Batch 2 - Class 309 - Topology - Graph coloring
zoom: send meeting Id and password
Start recording
Preclass Exercise:
- If you had infinitely stretchy pants, could you turn them inside out without lifting your feet off the ground?
- Answer: https://www.youtube.com/watch?v=H8qwqGjOlSE (around 7:50)
Attendance: Anika, Vansh, Rhea Chadha, Ryan Chadha, Adyant, Aarushi, Ekagra, Ayush, Dhriti, Advay, Tarush, Kabir, Vivaan, Nikhil, Raghav, Yatharth, Aneesh, Anant, Aarav, Siddhant, Siddharth
Class Notes:
Revision
- Cutting Cylinders and Mobius strips
- Tic-Tac-Toe
- Mathematical model of cylinder, mobius strip, torus etc.
- 3 Utilities problem
- Topological equivalence
Graph Coloring
- Explain the basic notion of planar graphs and a map
- Establish the correspondence between map and a graph
- Show the following pictures to the class and ask them to color it in minimum possible colors
- 2 color
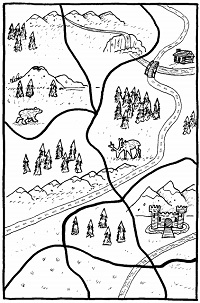
- 3 color
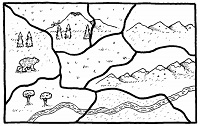
- 4 color
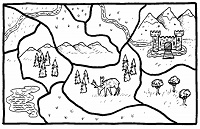
- How do we know these are the least number of colors required? (reasoning)
- Devise a graph that requires 5 colors
- No planar graph exists - this problem was posed in 1850 and was unsolved till 1976. This was solved computationally by taking a large set of possible combinations and reducing them to smaller graphs.
- Draw graphs corresponding to maps shown earlier
- Triangles imply 3 color requirement; fully connected 4 vertices imply 4 colors (though dependency chains can be more complex)
- For example, 5 vertices connected in a circle require 3 colors even though it seems alternating
- Practical Application: Students in a class take various subjects. What is the most efficient way to allocate periods to subjects so that all students can attend the classes
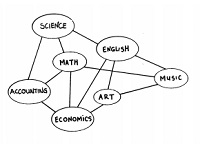
- Are there surfaces where 4 colors may not be enough?
- Show a mobius strip and ask kids to think about how many colors may be required?
- Answer: 6 colors
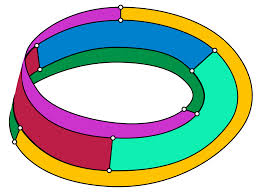
- Show kids a torus and ask kids to think about how many colors may be required?
- Answer: 7 colors (The first figure below folds into a torus; the second is another example of a torus map that requires 7 colors)
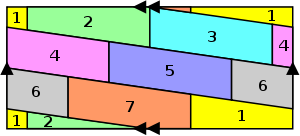

Homework Problem:
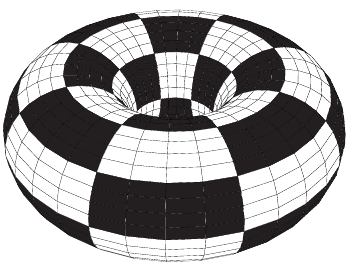
- Let us imagine a chess which has been folded in form of a torus, i.e. we have joined the left and right edges, and the top and bottom edges. It looks something like the following. How many positions can the bishop move to on a toroidal chess
References: